Browse by Topics
- English Worksheets
- Kid's Corner
- Numbers & Operations
- Addition
- Subtraction
- Multiplication
- Division
- Decimals
- Place Value
- Roman Numerals
- Skip Counting
- Odd & Even Numbers
- Patterns
- Cardinal & Ordinal Numbers
- Rounding Numbers
- Estimation of Numbers
- Estimation of Time & Money
- Counting & Cardinality
- Comparing Numbers
- Ordering Numbers
- Fractions
- Prime & Composite Numbers
- Squares & Cubes
- Divisibility Rules
- Factors & Multiples
- Data Handling
- Algebra
- Ratio
- Proportion
- Order of Operations
- Scientific Notation
- Exponents
- Algebraic Expressions
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Graphing Lines
- Point Slope Form
- Two Point Form
- Two Intercept Form
- Equations
- Identifying Functions
- Evaluating Functions
- Function Table
- Domain and Range
- Trigonometric Charts
- Quadrants
- Polynomials
- Measurement
- Geometry
- Word Problems
Medians and the Centroid of a triangle Worksheets
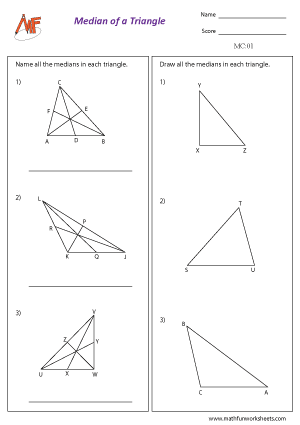
Medians and the centroid of a triangle are important concepts in geometry. A median is a line segment that connects a vertex of a triangle to the midpoint of the opposite side. Every triangle has three medians, and they all meet at a single point called the centroid. This point is the center of gravity, balancing the triangle perfectly if made from a uniform material.
To understand medians better, consider a triangle. The median starts at one vertex and ends at the midpoint of the opposite side. Each side of the triangle has its own median. These medians are not always the same length, but they always intersect at the centroid. The centroid divides each median into two parts. The distance from the vertex to the centroid is twice as long as the distance from the centroid to the midpoint of the opposite side.

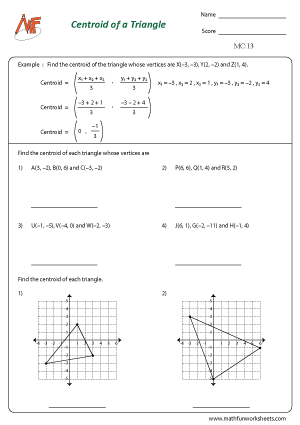
Moreover, the centroid has special properties. It is the center of mass for a triangle. This means that if a triangle were made from a uniform material, the centroid would be the balance point. It is also the point where the triangle’s three medians intersect. The centroid divides each median into a 2:1 ratio, with the longer part closer to the vertex.
Medians and the Centroid of a triangle worksheets free download pdf
Identify / Draw - Medians of a Triangle

Identify / Draw - Medians of a Triangle
Find the Unknown side of a Triangle

Find the Unknown side of a Triangle
Find the Equation of the Median

Find the Equation of the Median
Find the Centroid of the Triangle

Find the Centroid of the Triangle
Find the Missing Vertex - From Centroid

Find the Missing Vertex - From Centroid
Median and Centroid of a Triangle

Median and Centroid of a Triangle
Learning about medians and the centroid helps students better understand the balance and symmetry of shapes. It also prepares them for more advanced geometry topics. For example, understanding the centroid is useful in coordinate geometry, where it can be found using the average of the triangle’s vertex coordinates.
In conclusion, these worksheets provide a deeper understanding of the shape’s structure. By studying these concepts, students gain a better grasp of symmetry and geometry’s practical applications.