Browse by Topics
- English Worksheets
- Kid's Corner
- Numbers & Operations
- Addition
- Subtraction
- Multiplication
- Division
- Decimals
- Place Value
- Roman Numerals
- Skip Counting
- Odd & Even Numbers
- Patterns
- Cardinal & Ordinal Numbers
- Rounding Numbers
- Estimation of Numbers
- Estimation of Time & Money
- Counting & Cardinality
- Comparing Numbers
- Ordering Numbers
- Fractions
- Prime & Composite Numbers
- Squares & Cubes
- Divisibility Rules
- Factors & Multiples
- Data Handling
- Algebra
- Ratio
- Proportion
- Order of Operations
- Scientific Notation
- Exponents
- Algebraic Expressions
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Graphing Lines
- Point Slope Form
- Two Point Form
- Two Intercept Form
- Equations
- Identifying Functions
- Evaluating Functions
- Function Table
- Domain and Range
- Trigonometric Charts
- Quadrants
- Polynomials
- Measurement
- Geometry
- Word Problems
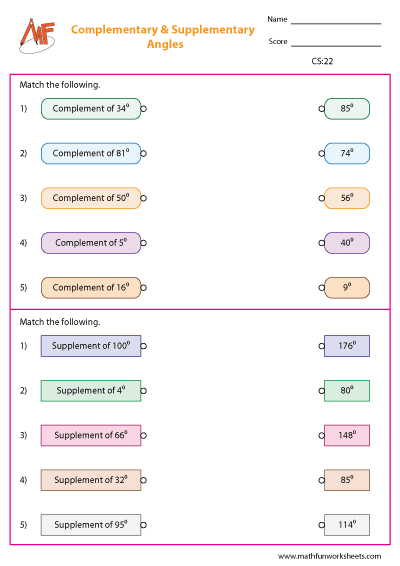
Complementary and Supplementary Angles Worksheets
Problems on complementary and supplementary angles are most easy to solve if you just remember the numbers 90 and 180. With the definitions given below, you will know how these numbers have been used in angles. You have ample problems to identify and calculate the missing measure of angles. Linear equations are also involved to calculate the measure of angles.
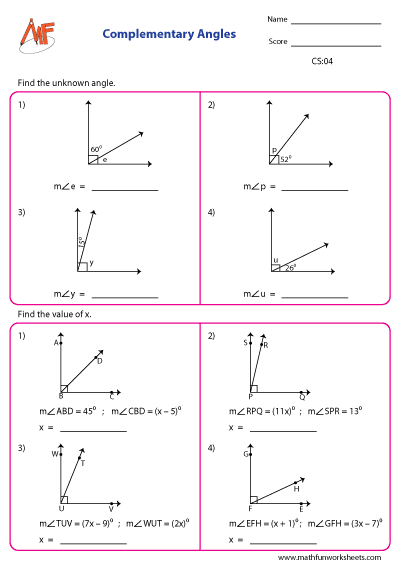
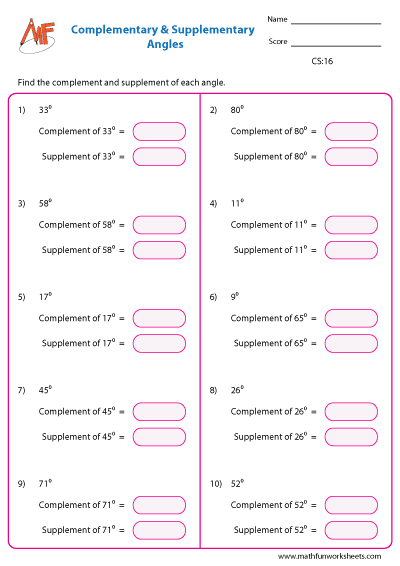
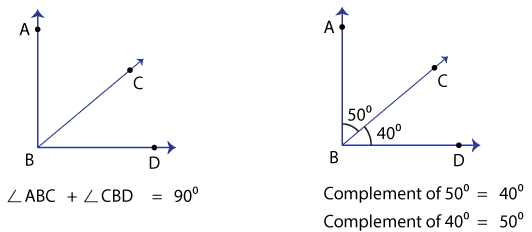
Complementary angles are two angles whose sum is 90°. So, the complement of 50° is (90 – 50), that is 40°. The complement of 40° is just the reverse, which is 50°.
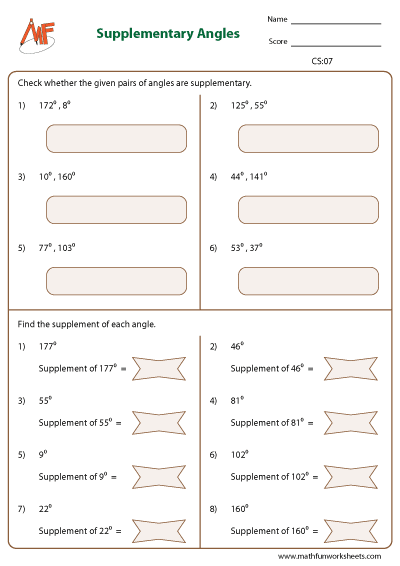
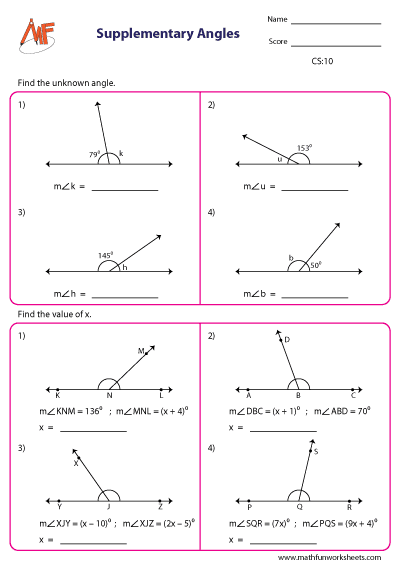
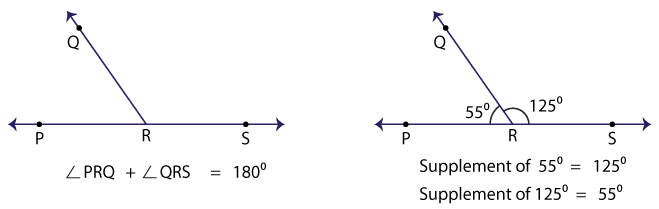
Supplementary angles are two angles whose sum is 180°. It can also be called linear pair of angles. The sum of a pair of linear angles is always 180°. Thus, the supplement of 55° is (180 – 55), that is 125°. The supplement of 125° is 55°, the vice versa.
The first few worksheets would deal with the basics. Then, to find missing angles. In the end, three exclusive worksheets have 5 word problems in each sheet. All you need to do is to form equations and solve for the unknown variable to find the measure of angles. All the best practice materials are available here for free download. Print them at once! Complementary and Supplementary Angles
-
-
Find the missing complementary angle
Find the missing complementary angle
-
-
Find the missing supplementary angle
Find the missing supplementary angle
-
Check complementary / supplementary angles
Check complementary / supplementary angles
-
Find the complement and supplement angle
Find the complement and supplement angle
-
Find complementary / supplementary angles
Find complementary / supplementary angles
-
-
